Rahasia Rumus-rumus “Cepat” Matematika
Oleh: Al JupriDulu, ketika saya masih baru menjadi mahasiswa baru tingkat pertama, saya berkenalan dengan salah seorang mahasiswa baru lainnya yang di kemudian hari menjadi teman baik saya. Ketika awal perkenalan, kami pun ngobrol kesana-kemari. Tanya sana-tanya sini. Jawab sana, jawab sini. Hingga ia pun akhirnya bercerita bahwaa nilai tes Matematika Dasar-nya, yaitu salah satu mata pelajaran yang diujikan di UMPTN*, adalah 100 alias benar semua.
Mendengar ceritanya tersebut, saya pun terkagum-kagum dibuatnya. Dalam pikiran saya, saya berkesimpulan “Wah ia pasti orang yang sangat pandai”. Rasa kagum saya mendorong rasa ingin tahu saya tentang pengetahuannya dalam matematika. Akhirnya, dalam masa awal perkenalan itu, saya ajak ia ngobrol tentang matematika yang sudah pernah kami pelajari ketika semasa SD sampai SMA dulu.
Dari obrolan tersebut, saya jadi tahu, ternyata ia benar-benar luas pengetahuan tentang matematika yang sudah dipelajarinya. Hingga akhirnya, mungkin untuk menunjukkan kepiawaiannya, ia mengajak saya adu cepat mengerjakan soal matematika.
Mendapat tantangan itu, sebenernya saya ngeper juga. Karena saya merasa tak sepandai dirinya. Namun, karena ini namanya juga bukan lomba dan bukan apa-apa, saya sih mau saja waktu itu. Soal-soal pun dipilih secara acak dari buku kumpulan soal-soal latihan tes UMPTN* dan EBTANAS** beberapa tahun sebelumnya yang masih rajin ia bawa ke mana-mana. Kemudian, adu cepat menyelesaikan soal matematika pun dimulai.
Bagaimana hasilnya? Siapa yang tercepat?
Ternyata benar, dalam beberapa menit saja, teman saya itu berhasil menyelesaikan semua soal yang sudah dipilih tadi (karena yang dipilih cuma 3 soal sih). Dan ia keluar sebagai yang tercepat, menjadi pemenang. Sedangkan saya, satu soal pun belum mampu saya selesaikan. Waktu itu, saya terlalu berkutat dengan soal nomor pertama yang lumayan sukar untuk ukuran saya waktu itu. Walau sudah dengan segenap kemampuan saya berusaha menyelesaikannya, tapi ternyata, sampai waktu habis belum ketemu juga. Saya pun mengakui kelebihan dan kehebatannya.
Dengan sedikit malu-malu, saya bertanya padanya tentang soal yang belum bisa saya selesaikan tersebut. Sambil saya tanyakan pula kenapa ia begitu cepat bisa menyelesaikan soal-soal tersebut. Soal yang waktu itu belum bisa saya selesaikan adalah seperti berikut ini.
Soal: Bila a + 1/a = 5, maka nilai dari a3 + 1/a3 =…
Dengan cepat teman saya itu pun menyelesaikan soal tersebut seperti berikut ini:
a3 + 1/a3 = (a + 1/a)3 – 3a.1/a(a + 1/a) = 53 – 3(5) = 125 – 15 = 110.
Melihat cara penyelesaiannya, saya hanya bisa melongo waktu itu. “Cuma satu baris? Padahal saya mencoba menyelesaikannya berbaris-baris, dan belum ketemu juga”, itu yang ada di pikiran saya. Kemudian, saya pun bertanya ke teman saya itu, kenapa cara pengerjaannya seperti itu?
Dengan senang hati, ia pun menjelaskan ke saya. Ia katakan bahwa, soal semacam tersebut dapat dengan mudah diselesaikan dengan rumus “cepat” berikut ini.
a3 + b3 = (a + b)3 – 3ab(a + b) ………………………………..(1)
Dengan mengganti b dengan 1/a, katanya, maka soal tadi dapat diselesaikan dengan cepat seperti yang sudah dikerjakannya tadi.
Saya yang tak terbiasa menggunakan rumus “cepat” ketika di SMA dulu, penasaran ingin tahu alasan kenapa rumus “cepat” tersebut bisa dipakai. Tapi sayang, teman saya itu tak memberi tahu saya. Malahan ia menambah lagi rumus cepat yang sudah ia ketahuinya, yaitu:
a3 – b3 = (a – b)3 + 3ab(a – b)……………………………….(2)
Akhirnya, ngobrol-ngobrol pun beres. Ia bergegas pulang menuju kost-kost-annya. Saya pun begitu, pulang dengan rasa penasaran yang mengganjal.
Di kost-kost-an, dengan penuh rasa penasaran ingin tahu, saya pun mengutak-atik rumus “cepat” yang telah ia gunakan tersebut. Setelah beberapa waktu lamanya, akhirnya, terpecahkan juga rahasia rumus “cepat” yang dipakai teman saya tersebut. Saya berhasil menelusuri asal-muasal rumus “cepat” tersebut, berhasil menguak rahasianya. (Duh rasanya begitu senang sekali, tak bisa saya ekspresikan dengan kata-kata).
Hasil penelusuran saya tersebut, setelah saya rapikan, seperti berikut ini.
(a + b)3 = (a + b)2(a + b)
= (a2 + 2ab + b2)( a + b)
= a3 + a2b + 2a2b + 2ab2 + b2a + b3
= a3 + b3 + 3a2b + 3ab2
= a3 + b3 + 3ab (a + b)
Jadi, (a + b)3 = a3 + b3 + 3ab (a + b).
Sehingga, a3 + b3 = (a + b)3 – 3ab (a + b). Rumus “cepat” (1) dapat saya buktikan kebenarannya. Kemudian, dengan cara serupa, saya pun berhasil menelusuri asal-muasal rumus “cepat” (2).
Walaupun apa yang telah saya lakukan tersebut sederhana, tapi bagi ukuran saya waktu itu adalah sesuatu yang menggembirakan hati, menyenangkan pikiran, dan memuaskan dahaga keingin-tahuan saya.
Sejak saat itu, bila ada rumus-rumus “cepat” yang saya temui di buku-buku bimbingan tes, saya pun terpacu untuk menelusuri asal-muasalnya. Dengan cara seperti itu, saya seringkali berhasil memecahkan rahasia rumus-rumus “cepat” yang selama ini beredar luas di kalangan siswa yang mengikuti bimbingan test.
Baiklah, segitu dulu saja ceritanya ya…, lain kali insya Allah saya akan membahas baik-buruknya penggunaan rumus “cepat” (Ada satu cerita yang sangat menggelikan tentang hal ini. Mau tahu? Silakan tunggu di postingan mendatang…). Sampai di sini dulu ya…, mudah-mudahan bermanfaat.
Sebagai bahan latihan untuk Anda, cobalah telusuri asal-muasal rumus-rumus “cepat” berikut ini.
- Persamaan garis yang melalui titik (0, a) dan (b, 0) adalah ax + by = ab.
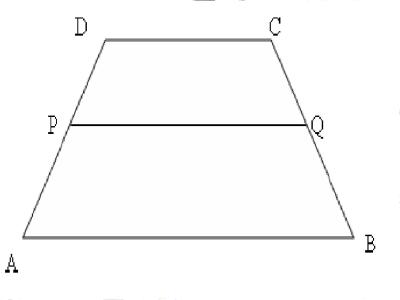
- Perhatikan gambar berikut. Panjang PQ dapat ditentukan dengan mudah, yaitu: PQ = (AP. DC + DP. AB)/(AD)
Catatan:
*UMPTN: Ujian Masuk Perguruan Tinggi Negeri (Saat ini namanya SPMB)
**EBTANAS: Evaluasi Belajar Tahap Akhir Nasional (Saat ini namanya UAN)
========================================================
Update: Artikel ini bisa juga dibaca di sini.
========================================================
Update:
Makin hari, makin banyak orang-orang yang secara tidak sopan menerbitkan ulang artikel saya ini. Mereka mempublikasi ulang tanpa menuliskan nama penulis dan sumbernya dan tidak memberi link sama sekali. Oleh karena itu, bila Anda menerbitkan ulang artikel ini, tolong minta ijin terlebih dulu ke saya. Bila Anda tidak minta ijin, saya tidak rela, saya tidak ikhlas, saya tidak mengijinkannya. Atas perhatiannya saya ucapkan terimakasih!!!!